Union Find - 并查集

Union-Find算法(并查集算法)是解决动态连通性（Dynamic Conectivity）问题的一种算法，"人以类聚,物以群分"

What is Union Find?

一种用来解决集合查询合并的数据结构，支持 O(1)find, O(1)union

查询 Find
- 确定某个元素x属于哪一个集合
合并 Union
- 将两个集合合并

应用场景

Computer Network
- 两个网络节点是否联通
- 最小的布线使得整个网络联通
Social Network
- Linkedin 两个用户可能认识的人
集合论

Union Find vs DFS

在对问题进行建模的时候，我们应该尽量想清楚需要解决的问题是什么! 因为模型中选择的数据结构和算法显然会根据问题的不同而不同!

Union Find - 给出两个节点，判断它们是否连通，如果连通，不需要给出具体的路径
DFS - 给出两个节点，判断它们是否连通，如果连通，需要给出具体的路径

Algorithm

Quick-Find

有点类似于染色的过程，每个节点一个颜色，然后相同的节点设置成相同的颜色。 quick-find算法十分直观符合简单的思考过程。

# Time : O(1)
def find(x):
    return root[x]

# Time : O(n)
def union(x, y):
    rootx = root[x]
    rooty = root[y]
    if rootx == rooty:
        return
    for i in xrange(len(root)):
        if root[i] == rootx:
            root[i] = rooty

每次添加新路径(Union)就是“牵一发而动全身”，想要解决这个问题，关键就是要提高union方法的效率，让它不再需要遍历整个数组。

Quick-Union

以树的思想，表示集合！！！
这是UF算法里最关键的思路，以树的形式表示集合，这样组织正好可是很高效的实现find和union!

# Time : O(Tree Height), Worst Case O(n)
# Recursion
def find(x):
    if root[x] == x:
        return x
    return find(root[x])

# Iteration
def find(x):
    while root[x] != x:
        x = root[x]
    return x

# Time : O(Tree Height), Worst Case O(n)
def union(x, y):
    rootx = find(x)
    rooty = find(y)
    if rootx != rooty: 判断两个Element在不在同一个集合当中
        root[rootx] = rooty

Weighted Quick-Union

既然树的高度成为制约时间复杂度的瓶颈，我们就想办法让树平衡！

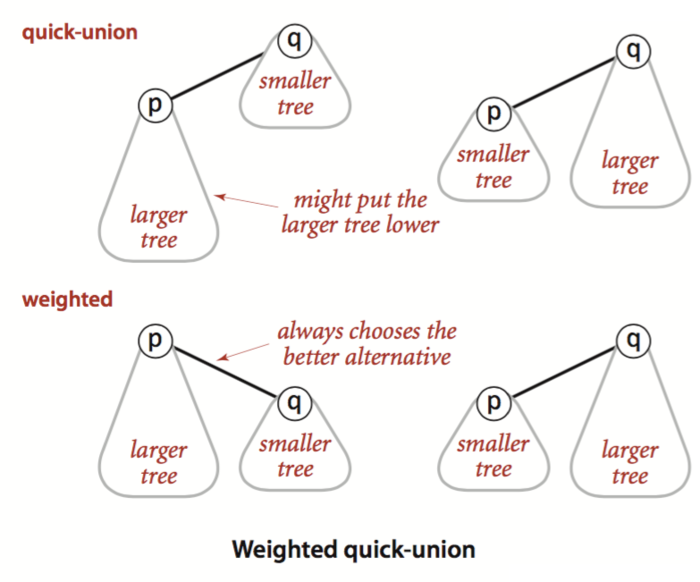
以Quick union为基础，我们额外利用一个size[]保存每一个联通集中对象的数量。
在调用union()的时候，我们总是把对象数目较少的联通集连接到对象数目较多的联通集中。
通过这种方式，我们可以在一定程度上缓解树的高度太大的问题，从而改善Quick union的时间复杂度。

# Time : O(logn)
def find(x):
    if root[x] == x:
        return x
    return find(root[x])

# Time : O(logn)
def union(x, y):
    rootx = find(x)
    rooty = find(y)
    if size[rootx] >= size[rooty]:
        root[rooty] = rootx
        size[rootx] += size[rooty]
    else:
        root[rootx] = rooty
        size[rooty] += size[rootx]

Path Compression

随着数据的增加，树的深度不断增加，性能会逐渐变差。这个时候，如果我们在计算一个node的root时，将node为根的树摘下来，挂在当前树的根结点上，会降低树的深度，也就是提高效率，降低时间复杂度。

# Path Compression 是在find的过程当中处理的
def find(x):
    if root[x] == x:
        return x

    # make every other node in path point to its grandparent.
    root[x] = find(root[x]) # Only one extra line

    return root[x]

Weighted Quick-Union With Path Compression

Proof is very difficult, But the algorithm is still simple!

# Weighted 是体现在Union的过程当中
# Time : Very Near to O(1)
def union(x, y):
    rootx = find(x)
    rooty = find(y)
    if size[rootx] >= size[rooty]:
        root[rooty] = rootx
        size[rootx] += size[rooty]
    else:
        root[rootx] = rooty
        size[rooty] += size[rootx]

Union Find