单序列动态规划

1 题型分析

• 输入是单序列，求前i个元素的某种性质
  • state : f[i]表示前i个位置/数字/字符，第i个...
  • function : f[i] = f[j]... (j < i)
  • initialize : f[0] ...
  • answer : f[n] ..
• 初始化dp[0]表示空序列
  • 坐标型dp[0]表示以$$a_i$$结尾的子序列性质

2 相邻约束型

256 Paint House

房子涂色，三种颜色，相邻的房子不能染成相同的颜色，求最小costs

• 状态:设油漆前i栋房子并且房子i-1是红色、蓝色、绿色的最小花费分别为 dp[i][0], dp[i][1], dp[i][2]
• 初始化dp[0][0], dp[0][1], dp[0][2]
• 答案是min{dp[N][0], dp[N][1], dp[N][2]}. 时间复杂度O(N), 空间复杂度O(N)

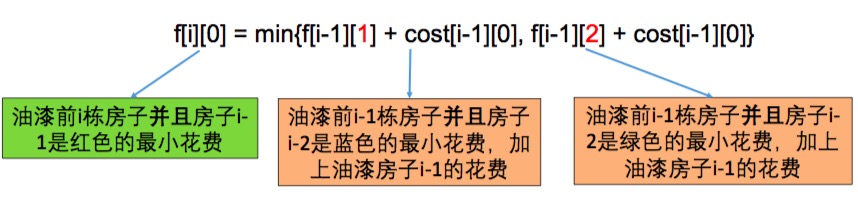
265 Paint House II

和I相同，但是房子可以涂k种颜色

• dp[i][j] = min{dp[i-1][k]}(k!=j) + cost[i-1][j]
• $$O(nk^2)$$ -> $$O(nk)$$, 每个元素的最小值？
• 只需要知道该序列的最小值和次小值

198 House Robber

偷房子里的钱，但是相邻的房子不能同时偷，求最大能偷多少钱？

• 确定状态：偷或者不偷最后一栋房子N-1
• dp[i] = max(dp[i-1], dp[i-2]+nums[i])

213 House Robber II

和I一样，但是房子成了一个圈(房子0和房子n-1不能同时偷)

• 分两个情况，不偷房子0和不偷房子n-1

3 最长序列系列

子数组和子序列(连续，不连续)

• Sub-array: contiguous elements in an array，仅有$$n^2$$个
• Sub-sequence: not necessarily contiguous，子序列有n!个
• 输入序列，求符合条件的最长子序列

300 Longest Increasing Subsequence

最长升序子序列(可不连续)

解法1 DP O($$n^2$$)

• dp[i]表示以a[i]结尾的最长上升子序列的长度
• 用DP将时间复杂度从$$O(n!)$$ => $$O(n^2)$$

解法2 Ending + Binary Search O(nlogn)

• ending数组代表的长度为i最小的结尾值
  • index 表示最长上升子序列的长度
  • value 表示该长度下的最小ending的值
  • ending 数组是单调递增的序列

class Solution(object):
    def lengthOfLIS(self, nums):
        if not nums: return 0
        n = len(nums)
        ends = [nums[0]]
        for i in xrange(1, n):
            if nums[i] > ends[-1]:
                ends.append(nums[i])
                continue
            # Binary Search >= target
            start, end = 0, len(ends)-1
            while start < end:
                mid = start + (end - start) // 2
                if ends[mid] < nums[i]:
                    start = mid + 1
                else:
                    end = mid
            ends[start] = nums[i]
        return len(ends)

354 Russian Doll Envelopes

解法2 DP O($$n^2$$) (TLE)

• 排序后，就化简成了最长上升子序列的问题

4 矩阵型

221. Maximal Square

• 求矩阵里，实心正方形个数？
  • How many Square? O($$n^3$$)

class Solution(object):
    def maximalSquare(self, matrix):
        if len(matrix) <= 0: return 0

        m, n = len(matrix), len(matrix[0])
        dp = [[0]*(n+1) for _ in xrange(m+1)]
        res = 0
        for i in xrange(m):
            for j in xrange(n):
                if matrix[i][j] == '1':
                    dp[i+1][j+1] = min(dp[i][j], dp[i+1][j], dp[i][j+1]) + 1
                    res = max(res, dp[i+1][j+1])
        return res * res