双序列动态规划

Created: 2018-04-03, Updated: 2018-04-05

题型分析

• Input输入参数都有两个序列或者字符串
• 都是二维DP

1 最长系列

LintCode 77. Longest Common Subsequence

最长公共子序列LCS，双序列动态规划。

• 状态:设dp[i][j]为A前i个字符A[0..i-1]和B前j个字符[0..j-1]的最长公共子串的长度

class Solution:
    def longestCommonSubsequence(self, A, B):
        m, n = len(A), len(B)
        if m == 0 or n == 0:
            return 0
        dp = [[0] * (n+1) for _ in xrange(m+1)]
        for i in xrange(1, m+1):
            for j in xrange(1, n+1):
                if A[i-1] == B[j-1]:
                    dp[i][j] = dp[i-1][j-1] + 1
                else:
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1])
        return dp[-1][-1]

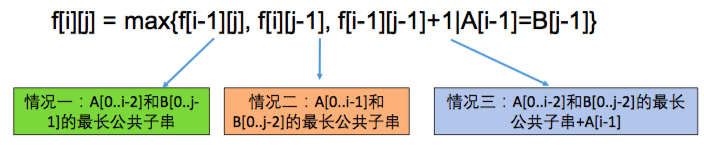
LintCode 79. Longest Common Substring

最长公共子串，和LCS最大的不同是要求substring，以ith个元素为ending

• 状态:设dp[i][j]为A前i个字符A[0..i-1]和B前j个字符[0..j-1]的最长公共子串的长度，且以A[i-1],B[i-1]结尾

2 存在性

97. Interleaving String

s1和s2交错是否能形成s3？

• 从Recursion写法出发，找到递推公式，再去分析初始化条件

class Solution(object):
    def isInterleave(self, s1, s2, s3):
        m, n, x = len(s1), len(s2), len(s3)
        if m + n != x:
            return False
        dp = [[False] * (n+1) for _ in xrange(m+1)]

        # Init
        dp[0][0] = True
        for i in xrange(1, m+1):
            if s1[i-1] == s3[i-1]:  dp[i][0] = dp[i-1][0]
        for j in xrange(1, n+1):
            if s2[j-1] == s3[j-1]:  dp[0][j] = dp[0][j-1]

        # Function
        for i in xrange(1, m+1):
            for j in xrange(1, n+1):
                if (dp[i-1][j] and s3[i+j-1] == s1[i-1]) or (dp[i][j-1] and s3[i+j-1] == s2[j-1]):
                    dp[i][j] = True

        return dp[-1][-1]

10. Regular Expression Matching

正则表达式，'.'可以匹配任意单个字符，'*'可以匹配零个或者多个predending字符。

44. Wildcard Matching

正则表达式，'?'可以匹配任意单个字符，'*'可以匹配任何字符包括空。

3 计数型

72. Edit Distance

求两个字符串的距离?

• 从最后一个字符出发
  • Insert
  • Delete
  • Replace
• 从Recursion的角度思考出发
  • 复杂度O($$4^n$$)

class Solution(object):
    def minDistance(self, word1, word2):
        m, n = len(word1), len(word2)
        dp = [[0] * (n+1) for _ in xrange(m+1)]
        # Init
        for i in xrange(1, m+1):
            dp[i][0] = i
        for j in xrange(1, n+1):
            dp[0][j] = j

        for i in xrange(1, m+1):
            for j in xrange(1, n+1):
                dp[i][j] = min(dp[i-1][j] + 1, dp[i][j-1] + 1, dp[i-1][j-1] + (word1[i-1] != word2[j-1]))

        return dp[-1][-1]

115. Distinct Subsequences