Binary Indexed Tree 树状数组
A Fenwick tree or binary indexed tree is a data structure that can efficiently update elements and calculate prefix sums in a table of numbers.
What is 树状数组?
也就是说,所谓树状数组,或称Binary Indexed Tree, Fenwick Tree,是一种用于高效处理对一个存储数字的列表进行更新及求前缀和的数据结构。
'''
Simple Prefix Sum Array
'''
PrefixSum # 前缀和数组
def update(idx, n):
# O(n), update idx-th num in the array
def rangeSum(idx1, idx2):
# O(1), calculate the sum from idx1-th to idx2-th in the arrayk
传统的数组单点修改的复杂度为 O(1),查询子段和的复杂度为 O(n) 前缀和数组单点修改的复杂度为 O(n),查询子段和的复杂度为 O(1)
- 树状数组的修改和查询子段和复杂度均为 O(logn)
- 所以在多组查询或动态查询时,用树状数组可以有效减小耗时,提高程序效率。
树状数组vs线段树
- 树状数组容易实现,代码量小,时间复杂度低,并且经过数学处理后也可以实现成段更新。线段树也可以做到和树状数组一样的效果,但是代码要复杂得多。
- 不过要注意,一般情况下树状数组能解决的问题线段树都能解决,反之有些线段树能解决的问题树状数组却不行。
树状数组的创建
从已知数组构建树状数组就是把线性的数组变成一棵树。那么,树状数组是如何把线性结构的数组变成一棵树的呢?以下以一个长度为8的数组为例:
原始数组:
A[1], A[2], A[3], A[4], A[5], A[6], A[7], A[8]
在修改和查询子段和时,很容易想到一种类似二分的想法来构建一棵树状的数组来保存原数组的所有信息。
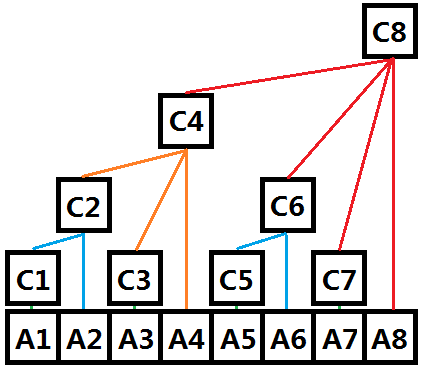
C1 = A1
C2 = C1 + A2 = A1 + A2
C3 = A3
C4 = C2 + C3 + A4 = A1 + A2 + A3 + A4
C5 = A5
C6 = C5 + A6 = A5 + A6
C7 = A7
C8 = C4 + C6 + C7 + A8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
从中可以发现,若结点的标号为 n ,则该结点的求和区域长度为 2k ,此处的 k 为 n 的二进制表示的末尾 0 的个数。
# 只保留n的二进制里最低位的1
2^k = n & (n ^ (n-1)) = n & (-n)
- 前n项和分别保存在n二进制表示的每个“1”表示
| i | 二进制 | 包含A的个数 |
|---|---|---|
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 1 |
| 6 | 0110 | 2 |
| 7 | 0111 | 1 |
| 8 | 1000 | 8 |
# Time : O(nlogn)
def build(self, nums):
n = len(nums)
# BIT 数组比原数组多一位!
A, C = nums, [0] * (n + 1)
for i in range(n):
k = i + 1 # Start From i+1
while k <= n:
C[k] += A[i]
k += (k & -k) # Next Parent Node
树状数组的更新
- C[i]的父节点为C[i + i & (-i)]
当我们修改A[i]的值时,记录变化,可以从C[i]往根节点一路上溯,调整这条路上的所有C[p]即可,这个操作的复杂度在最坏情况下就是树的高度即O(logn)。
def update(self, i, val):
diff, self.A[i] = val - self.A[i], val
i += 1 # Start From i+1
while i <= self.n:
self.C[i] += diff
i += (i & -i) # Next Parent Node
树状数组求和
- 而对于求数列的前n项和S[n],只需找到C[n]以前(包括C[n])的所有最大子树,把其根节点的C[c]加起来即可。
def sumRange(self, i, j):
res, j = 0, j + 1
while j: # 前j项和(j=j+1了,数组是从0开始index的!)
res += self.C[j]
j -= (j & -j) # Next Sum Node
while i: # 前i-1项和
res -= self.C[i]
i -= (i & -i)
return res
树状数组的应用
307. Range Sum Query - Mutable
树状数组的经典应用,支持更新数值的求区间和!
class NumArray(object):
def __init__(self, nums):
self.n = n = len(nums)
self.A, self.C = nums, [0] *(n + 1)
for i in xrange(n):
k = i + 1 # tip1:BIT index from 1
while k <= n:
self.C[k] += nums[i]
k += k & (-k)
def update(self, i, val):
diff = val - self.A[i]
self.A[i] = val # tip2 : remember to update original array
i += 1
while i <= self.n:
self.C[i] += diff
i += i & (-i)
def sumRange(self, i, j):
res = 0
j += 1
while j:
res += self.C[j]
j -= j & (-j)
while i: # tip3 : excluding i, so i do not need to +1
res -= self.C[i]
i -= i & (-i)
return res
308. Range Sum Query 2D - Mutable
class NumMatrix(object):
def __init__(self, matrix):
if not matrix:
return
m, n = len(matrix), len(matrix[0])
self.m, self.n = m, n
self.matrix = matrix
self.bit = [[0] * (n+1) for _ in xrange(m+1)]
for i in xrange(m):
for j in xrange(n):
self.build(i, j)
def build(self, row, col):
val = self.matrix[row][col]
i = row+1
while i <= self.m:
j = col + 1
while j <= self.n:
self.bit[i][j] += val
j += j & (-j)
i += i & (-i)
def update(self, row, col, val):
diff = val - self.matrix[row][col]
self.matrix[row][col] = val
i = row+1
while i <= self.m:
j = col + 1 # Init j in the loop
while j <= self.n:
self.bit[i][j] += diff
j += j & (-j)
i += i & (-i)
def getSum(self, row, col):
i = row+1
res = 0
while i:
j = col + 1
while j:
res += self.bit[i][j]
j -= j & (-j)
i -= i & (-i)
return res
def sumRegion(self, row1, col1, row2, col2):
return self.getSum(row2, col2) - self.getSum(row1-1, col2) - self.getSum(row2, col1-1) + self.getSum(row1-1, col1-1)
315. Count of Smaller Numbers After Self
Binary Indexed Tree & Fenwick Tree
- 对原数组nums进行离散化处理(排序+去重),将nums从实数范围映射到 [1, len(set(nums))],记得到的新数组为iNums
idxes = {}
for k, v in enumerate(sorted(set(nums))):
idxes[v] = k + 1
iNums = [idxes[x] for x in nums]
# iNums 相当于重新映射后的Array,其间数值的相对大小没有改变,
# 但是值总的范围映射到了[0, n]这样就可以作为BIT的index了!!
- 从右向左遍历iNums,对树状数组的iNums[i]位置执行+1操作,然后统计(0, iNums[i])的区间和,也可以用线段树
- 把计数问题转化成了求区间和的问题!
class FenwickTree(object):
def __init__(self, n):
self.n = n
self.BIT = [0] * (n+1)
def add(self, i, val):
while i <= self.n:
self.BIT[i] += val
i += i & -i
def sum(self, i):
res = 0
while i:
res += self.BIT[i]
i -= i & -i
return res
class Solution(object):
def countSmaller(self, nums):
if not nums: return []
idxs = {}
for k, v in enumerate(sorted(set(nums))):
idxs[v] = k + 1
n = len(nums)
ftree = FenwickTree(n)
res = []
for i in xrange(n-1, -1, -1):
res.append(ftree.sum(idxs[nums[i]]-1))
ftree.add(idxs[nums[i]], 1)
return res[::-1]
493. Reverse Pairs
TODO