综合型动态规划
LintCode 91. Minimum Adjustment Cost
调整数组中每个元素的大小,使得相邻元素的difference小于target,求最小的调整和!(每个元素的大小在[0, 100]之间)
- 从最后一步出发寻找状态
- A是Original Array,B是Adjusted Array
- 最后一步将A改成B,A[n-1]改成X,这一步代价是|A[n-1]-X|
- 限制是|X-B[n-2]| < = Target
- 序列+状态
- 设状态dp[i][j]为将A前i个元素改成B的最小代价,确保前i个改好的元素中任意两个相邻的元素的差不超过Target,并且A[i-1]改成j
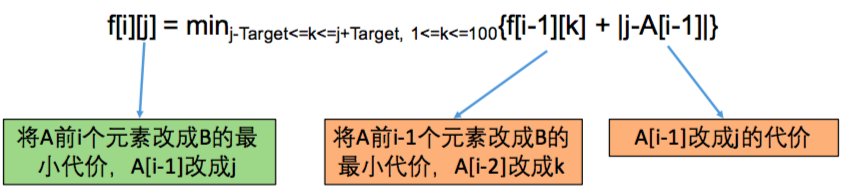
- 设状态dp[i][j]为将A前i个元素改成B的最小代价,确保前i个改好的元素中任意两个相邻的元素的差不超过Target,并且A[i-1]改成j
class Solution:
def MinAdjustmentCost(self, A, target):
# write your code here
m = len(A)
dp = [[0] * 101 for _ in xrange(m+1)]
// Init
for i in xrange(101):
dp[1][i] = abs(A[0] - i)
for i in xrange(2, m+1):
for j in xrange(1, 101):
dp[i][j] = float('inf')
for k in xrange(max(1, j-target), min(100, j+target)+1):
dp[i][j] = min(dp[i][j], dp[i-1][k] + abs(A[i-1]-j))
return min(dp[-1][1:])
LintCode 89. k Sum
从Array中选k个数,使得总和为target,求多少种方式?
- 最后一个元素要不要出发,寻找状态
- dp[i][k][s]表示有多少种方法可以在前i个数中选出k个,使得它们的和是s
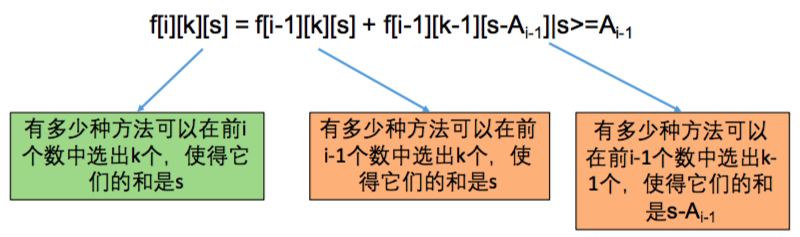
- dp[i][k][s]表示有多少种方法可以在前i个数中选出k个,使得它们的和是s