Prefix Sum 前缀和

给定一个数组A[1..n]，前缀和数组PrefixSum[1..n]定义为： PrefixSum[i] = A[0]+A[1]+...+A[i-1]；

例如：A[5,6,7,8] --> PrefixSum[5,11,18,26] PrefixSum[0] =A[0] ; PrefixSum[1] =A[0] + A[1] ; PrefixSum[2] =A[0] + A[1] + A[2] ; PrefixSum[3] =A[0] + A[1] + A[2] + A[3] ;

1 Range Sum 区间求和

303. Range Sum Query - Immutable

如果给定数组不变，求任意区间的和

class NumArray(object):
    # Time : O(n), Space : O(n)
    def __init__(self, nums):
        self.preSum = [0]
        n = len(nums)
        s = 0
        for i in xrange(n):
            s += nums[i]
            self.preSum.append(s)
    # Time : O(1)
    def sumRange(self, i, j):
        return self.preSum[j+1] - self.preSum[i]

304. Range Sum Query 2D - Immutable

presum扩展到2D的应用

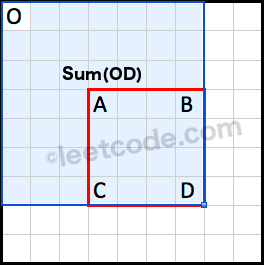
class NumMatrix(object):
    # Time : O(mn), Space : O(mn)
    def __init__(self, matrix):
        if not matrix:
            self.dp = []
            return
        m, n = len(matrix), len(matrix[0])
        self.dp = [[0] * (n+1) for _ in xrange(m+1)]
        dp = self.dp
        for i in xrange(1, m+1):
            for j in xrange(1, n+1):
                dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + matrix[i-1][j-1]

    # Time : O(1)
    def sumRegion(self, row1, col1, row2, col2):
        if not self.dp:
            return 0
        return self.dp[row2+1][col2+1] - self.dp[row2+1][col1] - self.dp[row1][col2+1] + self.dp[row1][col1]

363. Max Sum of Rectangle No Larger Than K

矩阵有多少个子矩阵? O($$n^2$$ * $$n^2$$) = O($$n^4$$)

解法1.Naive

计算矩阵和O($$n^2$$), 总Time:O($$n^6$$)

解法2.PreSum优化矩阵和计算

计算矩阵和O(1), 总Time:O($$n^4$$) Space:O($$n^2$$)用来存左上角(0,0)->右下角(i,j)的矩阵和

class Solution(object): # TLE
    def maxSumSubmatrix(self, matrix, k):
        if not matrix: return 0
        m, n = len(matrix), len(matrix[0])

        # PreSum matrix
        dp = [[0] * (n+1) for _ in xrange(m+1)]
        for i in xrange(1, m+1):
            for j in xrange(1, n+1):
                dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + matrix[i-1][j-1]

        def sumRegion(row1, col1, row2, col2):
            return dp[row2+1][col2+1] - dp[row2+1][col1] - dp[row1][col2+1] + dp[row1][col1]

        res = -float('inf')
        for i in xrange(m):
            for j in xrange(n):
                for li in xrange(i, m):
                    for lj in xrange(j, n):
                        s = sumRegion(i, j, li, lj)
                        if s <= k:
                            res = max(res, s)
        return res

解法3.极其巧妙！

1 pre-processing 预处理 1D

从上到下做1D的preSum, O($$n^2$$)

2 任意取两行压缩成一个Array

瞬间把一个2D的matrix经过O($$n^2$$)转化成了1D的array

3 求一个Array里不大于k的连续subarray

新问题：求数组里不大于k的连续subarray O(nlogn)

TODO : python没有treeset的怎么搞？

2 Subarray 子序列和问题

preSum + HashTable

560. Subarray Sum Equals K

一共有O($$n^2$$)个subarray，求和是O($$n$$),总共是O($$n^3$$)

解法1.preSum优化求和

优化求和过程，但是结果O($$n^2$$)还是TLE

解法2.HashTable, O(n)

A[0] + A[1] + ... + A[j] = V

preSum[j] - preSum[i] = V 有点类似Two Sum，查询是否在preSum

class Solution(object):
    def subarraySum(self, nums, k):
        preSum = defaultdict(int)
        s = count = 0
        preSum[0] = 1
        for n in nums:
            s += n
            if (s - k) in preSum:
                count += preSum[s - k]
            sums[s] += 1
        return count

325. Maximum Size Subarray Sum Equals k

求最长的子序列和为k, preSum + HashTable

class Solution(object):
    def maxSubArrayLen(self, nums, k):
        if not nums: return 0

        preSum = collections.defaultdict(int)
        preSum[0] = -1
        s = res = 0
        for i, n in enumerate(nums):
            s += n
            pre = s - k
            if pre in preSum:
                res = max(res, i-preSum[pre])

            if s not in preSum:
                preSum[s] = i
        return res

Prefix Sum